Gradient basics#
# This is only valid when the package is not installed
import sys
sys.path.append('../../') # two folders up
import DeepINN as dp
Using default backend: PyTorch
Using Pytorch: 2.0.1+cu117
from torch import nn
import torch
Test 1#
x = torch.tensor([2.0], requires_grad = True)
print("x:", x)
y = x**2 + 1
print("y:", y)
x: tensor([2.], requires_grad=True)
y: tensor([5.], grad_fn=<AddBackward0>)
\[y=x^2 +1\]
\[\frac{dy}{dx} = 2x\]
# Calculate the gradient manually using torch.autograd.grad()
gradient = torch.autograd.grad(y, x, create_graph=True, retain_graph=True)[0]
print("Gradient (dy/dx):", gradient)
Gradient (dy/dx): tensor([4.], grad_fn=<MulBackward0>)
torch.autograd.grad(gradient, x, retain_graph=True)[0]
tensor([2.])
jacobian = dp.constraint.Jacobian(x, y)(0,0)
# jacobian_matrix = jacobian(0, 1)
jacobian
tensor([4.], grad_fn=<MulBackward0>)
dp.constraint.Jacobian(x, jacobian)(0,0)
tensor([2.], grad_fn=<MulBackward0>)
A note for the future.#
If we need to use the same graph to computer more gradients then we need to use retain_graph=True We need to investigate whether we need this.
here we confirmed that both compute the same gradient.
1D tensor with multiple values.#
# Define a simple neural network for demonstration
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.linear = nn.Linear(2, 1) # automatic weights initialisation
def forward(self, x):
return self.linear(x)
# Create random input tensor
X = torch.tensor([1.0, 2.0], requires_grad=True)
X, X.size()
(tensor([1., 2.], requires_grad=True), torch.Size([2]))
# Instantiate the neural network
net = Net()
# Forward pass
y = net(X)
y
tensor([1.5027], grad_fn=<AddBackward0>)
# pytorch gradient
# Calculate the gradient manually using torch.autograd.grad()
gradient = torch.autograd.grad(y, X, retain_graph=True)[0]
print("Gradient (dy/dx):", gradient)
Gradient (dy/dx): tensor([0.6726, 0.4256])
jacobian = dp.constraint.Jacobian(X, y)(0,0)
jacobian
tensor([0.6726, 0.4256], grad_fn=<SqueezeBackward1>)
Again we verified that dp and torch are giving the same results.
Let us do a manual forward prop for fun.
# Manually compute gradient
weights = net.linear.weight
biases = net.linear.bias
output = torch.matmul(X, weights.t()) + biases
y, output # notice both are same. ok I am stupid
(tensor([1.5027], grad_fn=<AddBackward0>),
tensor([1.5027], grad_fn=<AddBackward0>))
2D tensor#
# Create a 2D input tensor
X = torch.tensor([[1.0, 2.0], [3.0, 4.0]], requires_grad=True)
print("X:\n", X)
X:
tensor([[1., 2.],
[3., 4.]], requires_grad=True)
# Define a function that operates on the input tensor
def func(x):
return torch.sin(x)
# Compute the output tensor
y = func(X)
print("y:\n", y)
y:
tensor([[ 0.8415, 0.9093],
[ 0.1411, -0.7568]], grad_fn=<SinBackward0>)
# pytorch gradient
# Calculate the gradient manually using torch.autograd.grad()
gradient = torch.autograd.grad(y, X, grad_outputs=torch.ones_like(y), retain_graph=True)[0]
print("Gradient (dy/dx):", gradient)
Gradient (dy/dx): tensor([[ 0.5403, -0.4161],
[-0.9900, -0.6536]])
# Instantiate the Jacobian module
jacobian = dp.constraint.Jacobian(X, y)
says the first column denotes x-coodinates and the the second column denotes the y-coordintes.
# dy/dx-coordinates, dy/dy-coordinates
jacobian(0, 0), jacobian(0, 1)
(tensor([[ 0.5403],
[-0.9900]], grad_fn=<IndexBackward0>),
tensor([[-0.4161],
[-0.6536]], grad_fn=<IndexBackward0>))
Gradients with actual geometry#
# Let us make a simple rectangle
X = dp.spaces.R2('x') # 2D space stencil
R = dp.domains.Parallelogram(X, [0,0], [1,0], [0,1])
collocation_points = dp.samplers.RandomUniformSampler(R, n_points = 100)
dp.utils.scatter(X, collocation_points)
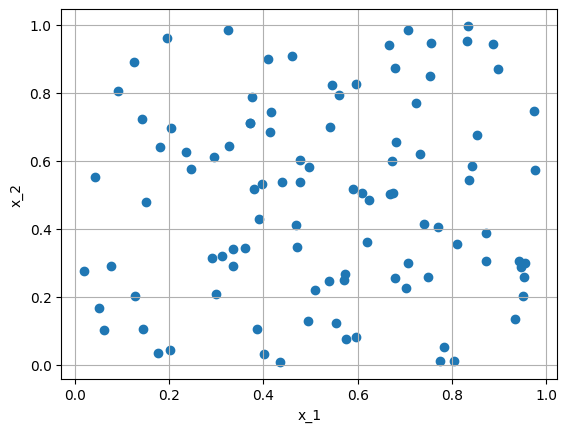
# sample collcocation points
collocation_points = dp.constraint.PDE(geom = R,
sampling_strategy= "random",
no_points = 100)
collocation_points_sampled = collocation_points.sampler_object().sample_points().as_tensor
collocation_points_sampled.size()
torch.Size([100, 2])
collocation_points_labels = collocation_points.sample_labels(collocation_points_sampled).unsqueeze(1)
collocation_points_labels.size()
torch.Size([100, 1])
import matplotlib.pyplot as plt
# The variation in BCs based on the provided function : lambda X: X[:,0]**2
plt.scatter(collocation_points_sampled[:,0], collocation_points_sampled[:,1], c = collocation_points_labels, cmap=plt.get_cmap('plasma',10))
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x7b9c52997580>
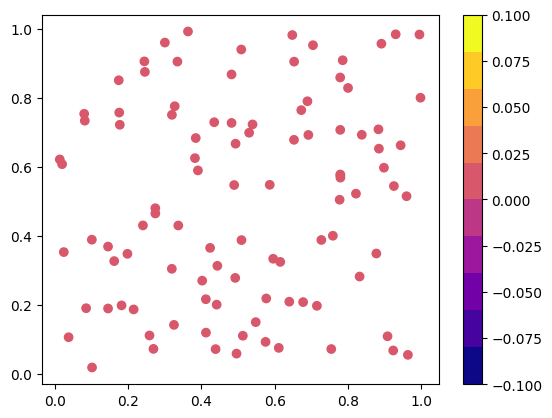
collocation_points_sampled.requires_grad = True # enable chain rule
# to differentiate a function, we need an actual function/neural network which take the collocation_points_sampled as the input and outputs the y
y = (collocation_points_sampled[:,0] ** 2).unsqueeze(1) + collocation_points_labels
y.size()
torch.Size([100, 1])
# pytorch gradient
# Calculate the gradient manually using torch.autograd.grad()
gradient = torch.autograd.grad(y, collocation_points_sampled, grad_outputs=torch.ones_like(y), retain_graph=True)[0]
print("Gradient (dy/dx):", gradient)
Gradient (dy/dx): tensor([[0.6733, 0.0000],
[0.6685, 0.0000],
[1.0176, 0.0000],
[1.6641, 0.0000],
[1.9967, 0.0000],
[0.6386, 0.0000],
[1.2306, 0.0000],
[1.7671, 0.0000],
[1.3454, 0.0000],
[1.8883, 0.0000],
[1.2225, 0.0000],
[0.8830, 0.0000],
[1.5180, 0.0000],
[1.6009, 0.0000],
[1.1501, 0.0000],
[1.4308, 0.0000],
[1.0261, 0.0000],
[1.5584, 0.0000],
[1.1730, 0.0000],
[0.7687, 0.0000],
[0.8867, 0.0000],
[1.4550, 0.0000],
[0.8041, 0.0000],
[1.5583, 0.0000],
[1.5580, 0.0000],
[1.7970, 0.0000],
[0.5377, 0.0000],
[0.6538, 0.0000],
[1.7832, 0.0000],
[0.4909, 0.0000],
[0.8772, 0.0000],
[0.5479, 0.0000],
[0.1592, 0.0000],
[0.0740, 0.0000],
[0.3507, 0.0000],
[0.9643, 0.0000],
[0.0257, 0.0000],
[0.5479, 0.0000],
[1.2799, 0.0000],
[1.7555, 0.0000],
[0.0478, 0.0000],
[1.9280, 0.0000],
[0.6001, 0.0000],
[0.9786, 0.0000],
[0.3538, 0.0000],
[1.6759, 0.0000],
[0.8473, 0.0000],
[1.0966, 0.0000],
[0.3954, 0.0000],
[0.9916, 0.0000],
[0.3232, 0.0000],
[1.4093, 0.0000],
[1.1539, 0.0000],
[1.3791, 0.0000],
[1.8612, 0.0000],
[1.5549, 0.0000],
[1.1919, 0.0000],
[0.9863, 0.0000],
[1.0187, 0.0000],
[0.9845, 0.0000],
[1.5591, 0.0000],
[0.8240, 0.0000],
[0.3481, 0.0000],
[1.8477, 0.0000],
[1.0604, 0.0000],
[1.3063, 0.0000],
[1.8167, 0.0000],
[0.5160, 0.0000],
[0.2010, 0.0000],
[0.6498, 0.0000],
[1.6442, 0.0000],
[0.4801, 0.0000],
[1.3056, 0.0000],
[0.1697, 0.0000],
[0.2895, 0.0000],
[0.9645, 0.0000],
[1.3555, 0.0000],
[0.8697, 0.0000],
[0.7806, 0.0000],
[1.7696, 0.0000],
[0.2021, 0.0000],
[0.8245, 0.0000],
[0.3633, 0.0000],
[1.2962, 0.0000],
[0.0385, 0.0000],
[1.0791, 0.0000],
[1.5716, 0.0000],
[0.1625, 0.0000],
[0.2896, 0.0000],
[1.5592, 0.0000],
[1.9910, 0.0000],
[0.7264, 0.0000],
[1.9206, 0.0000],
[0.6380, 0.0000],
[1.8515, 0.0000],
[1.3841, 0.0000],
[1.5092, 0.0000],
[0.7644, 0.0000],
[0.4880, 0.0000],
[0.4294, 0.0000]])
# Instantiate the Jacobian module
jacobian = dp.constraint.Jacobian(collocation_points_sampled, y)
# dy/dx-coordinates,
jacobian(i = 0, j = 0)
tensor([[0.6733],
[0.6685],
[1.0176],
[1.6641],
[1.9967],
[0.6386],
[1.2306],
[1.7671],
[1.3454],
[1.8883],
[1.2225],
[0.8830],
[1.5180],
[1.6009],
[1.1501],
[1.4308],
[1.0261],
[1.5584],
[1.1730],
[0.7687],
[0.8867],
[1.4550],
[0.8041],
[1.5583],
[1.5580],
[1.7970],
[0.5377],
[0.6538],
[1.7832],
[0.4909],
[0.8772],
[0.5479],
[0.1592],
[0.0740],
[0.3507],
[0.9643],
[0.0257],
[0.5479],
[1.2799],
[1.7555],
[0.0478],
[1.9280],
[0.6001],
[0.9786],
[0.3538],
[1.6759],
[0.8473],
[1.0966],
[0.3954],
[0.9916],
[0.3232],
[1.4093],
[1.1539],
[1.3791],
[1.8612],
[1.5549],
[1.1919],
[0.9863],
[1.0187],
[0.9845],
[1.5591],
[0.8240],
[0.3481],
[1.8477],
[1.0604],
[1.3063],
[1.8167],
[0.5160],
[0.2010],
[0.6498],
[1.6442],
[0.4801],
[1.3056],
[0.1697],
[0.2895],
[0.9645],
[1.3555],
[0.8697],
[0.7806],
[1.7696],
[0.2021],
[0.8245],
[0.3633],
[1.2962],
[0.0385],
[1.0791],
[1.5716],
[0.1625],
[0.2896],
[1.5592],
[1.9910],
[0.7264],
[1.9206],
[0.6380],
[1.8515],
[1.3841],
[1.5092],
[0.7644],
[0.4880],
[0.4294]], grad_fn=<IndexBackward0>)
#dy/dy-coordinates
jacobian(i = 0, j = 1)
tensor([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]], grad_fn=<IndexBackward0>)
hessian = dp.constraint.Jacobian(collocation_points_sampled, jacobian(i = 0, j = 1)
)
hessian(i = 0, j = 0)
tensor([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]], grad_fn=<IndexBackward0>)
hessian(i = 0, j = 1)
tensor([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]], grad_fn=<IndexBackward0>)
